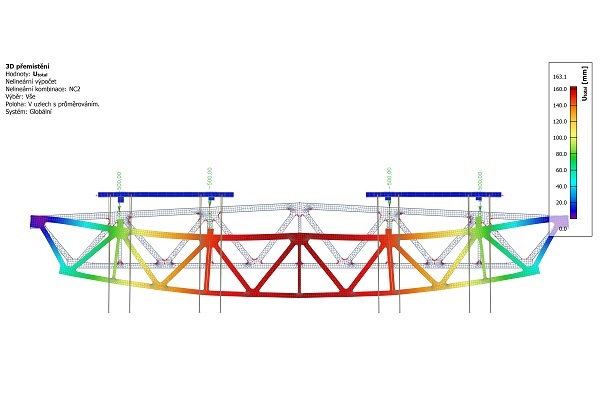
Lectures:
1. Direct stiffness method I.: The principle of the method, the degree of deformational uncertainty of planar structures.
2. Direct stiffness method II.: Analysis of the direct beam with different supports, local coordinate system, its selection and transformation into the global coordinate system.
3. Direct stiffness method III.: Analysis of the beam system, calculation of the deformation state, determination of components of internal forces of the members and reaction components.
4. Direct stiffness method IV.: Creation of system of equations. Solving the system of equations. Matrix band and sparse systems of linear equations.
5. Direct stiffness method V.: Solution of continuous beams, rectangular and angular plane frames, planar trusses by direct stiffness method. Force and strain loads. Irregular temperature change.
6. Direct stiffness method VI.: Spatial beam systems and planar frames transversally loaded.
7. Transmission matrices: Derivation, load assignment, demonstration examples.
8. Geometric non-linear solution of trusses: Derivation, direct stiffness method and its application, iterative solution of geometrically non-linear calculation of planar truss structure according to theory of IInd order, demonstration examples.
9. Stability of compressed members using the principle of virtual works: Stability of slender compressed members using the principle of virtual works and theory of IInd order, derivation, application, iterative solution of buckling load bearing capacity of slender pressed rods, comparison with exact Euler analytical solution, demonstration examples.
10. Eigenvalues of matrices and eigenvectors: Introduction, numerical methods for solving eigenvalues of matrices and corresponding eigenvectors, partial and complete problem of eigenvalues, practical use in the tasks of building mechanics.
11. Eigenmodes and eigenfrequencies of free vibration: Introduction to the problem, orthogonality of its eigenmodes, standardized eigenmodes. Determination of eigenfrequencies and eigenmodes of free vibration in simple constructions.
12. Random variables and probabilistic simulation calculations I.: Random variable - discrete random variable, continuous random variable. Parametric probability distribution, nonparametric (empirical) probability distribution.
13. Random variables and probabilistic simulation calculations II.: Generate random variables in Matlab. Probabilistic assessment of the support element.
14. Sample solution for selected tasks.
1. Direct stiffness method I.: The principle of the method, the degree of deformational uncertainty of planar structures.
2. Direct stiffness method II.: Analysis of the direct beam with different supports, local coordinate system, its selection and transformation into the global coordinate system.
3. Direct stiffness method III.: Analysis of the beam system, calculation of the deformation state, determination of components of internal forces of the members and reaction components.
4. Direct stiffness method IV.: Creation of system of equations. Solving the system of equations. Matrix band and sparse systems of linear equations.
5. Direct stiffness method V.: Solution of continuous beams, rectangular and angular plane frames, planar trusses by direct stiffness method. Force and strain loads. Irregular temperature change.
6. Direct stiffness method VI.: Spatial beam systems and planar frames transversally loaded.
7. Transmission matrices: Derivation, load assignment, demonstration examples.
8. Geometric non-linear solution of trusses: Derivation, direct stiffness method and its application, iterative solution of geometrically non-linear calculation of planar truss structure according to theory of IInd order, demonstration examples.
9. Stability of compressed members using the principle of virtual works: Stability of slender compressed members using the principle of virtual works and theory of IInd order, derivation, application, iterative solution of buckling load bearing capacity of slender pressed rods, comparison with exact Euler analytical solution, demonstration examples.
10. Eigenvalues of matrices and eigenvectors: Introduction, numerical methods for solving eigenvalues of matrices and corresponding eigenvectors, partial and complete problem of eigenvalues, practical use in the tasks of building mechanics.
11. Eigenmodes and eigenfrequencies of free vibration: Introduction to the problem, orthogonality of its eigenmodes, standardized eigenmodes. Determination of eigenfrequencies and eigenmodes of free vibration in simple constructions.
12. Random variables and probabilistic simulation calculations I.: Random variable - discrete random variable, continuous random variable. Parametric probability distribution, nonparametric (empirical) probability distribution.
13. Random variables and probabilistic simulation calculations II.: Generate random variables in Matlab. Probabilistic assessment of the support element.
14. Sample solution for selected tasks.