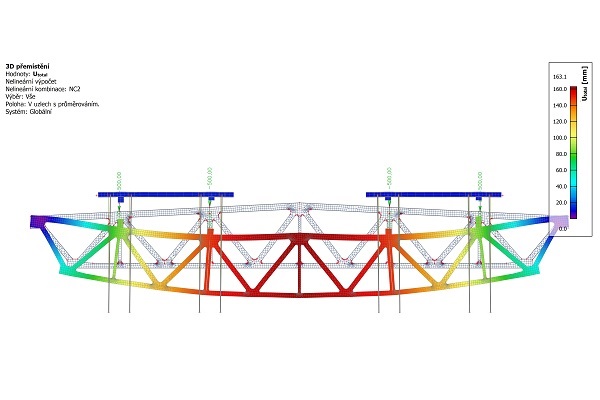
- Introduction, force method and displacement method.
- Energy methods, basic principles of FEM.
- Relationship between FEM and displacement methods.
- Example of deriving a finite element stiffness matrix.
- Isoparametric finite elements.
- Accuracy and convergence of FEM solutions.
- Idealization of computational models, influence on results.
- Nonlinear analysis with FEM.
- Physical nonlinearity - plasticity.
- Stability, imperfections and geometric nonlinearity.
- Contact tasks.
- Structure dynamics problems.
- Modeling of heat conduction.
- Coupled analysis with FEM.
- Energy methods, basic principles of FEM.
- Relationship between FEM and displacement methods.
- Example of deriving a finite element stiffness matrix.
- Isoparametric finite elements.
- Accuracy and convergence of FEM solutions.
- Idealization of computational models, influence on results.
- Nonlinear analysis with FEM.
- Physical nonlinearity - plasticity.
- Stability, imperfections and geometric nonlinearity.
- Contact tasks.
- Structure dynamics problems.
- Modeling of heat conduction.
- Coupled analysis with FEM.